티스토리 뷰
문제 : https://oj.uz/problem/view/FXCUP3_key
어느 저택에 N개의 방이 있다.
i번 방에 들어가기 위해서는 i번 열쇠가 필요하다.
그리고 i번 방 안에는 추가로 \(In_i\)번 열쇠가 있어서, i번 방 안에 들어간다면 \(In_i\)번 방에도 들어갈 수 있게 된다.
모든 i에 대하여, i번 열쇠 하나를 가지고 저택에 들어간 경우, 들어갈 수 있는 모든 방 번호를 구하는 문제
인터렉션
void TakeKey(int K)K번 열쇠를 준비한다.
여러 번 호출하여 여러 개의 열쇠를 가질 수 있지만, 같은 번호의 열쇠는 한 개만 가질 수 있다.
int Explore()TakeKey()를 통해 받은 열쇠를 가지고, 저택에 들어간 후, 들어갈 수 있는 방의 개수를 반환한다.
Explore() 함수를 호출한 경우, TakeKey()를 통해 받은 열쇠는 모두 사라진다.
최대 10000번 호출 가능
void Report(int Key, int Room)Key번 열쇠를 가지고 저택에 들어가면, 최종적으로 Room번 방에 들어갈 수 있다고 기록하는 함수
제약
- 만점 기준 N은 최대 1000
풀이
저택과 방에 들어있는 열쇠로 결국 그래프 구조가 된다.
우선 사이클이 없는 경우만 고려해보자
그러면 저택은 아래와 같이 포레스트 구조가 일 것이다.
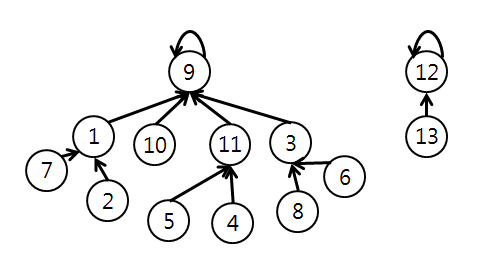
모든 i에 대하여, TakeKey(i)와 Explore()를 호출한다.
그러면 Explore()의 반환값은 tree의 depth와 같다.
반환값을 이용하여 리스트 자료구조를 이용하여, 같은 depth 끼리 그룹화를 해보자
- vec[1] = {9,1,2}
- vec[2] = {1,3,10,11,13}
- vec[3] = {2,4,5,6,7,8}
vec[2]의 한 원소를 x라 하자.
x의 부모는 vec[1]에서 찾을 수 있다.
1의 부모를 찾기 위해, TakeKey(9)와 TakeKey(1)을 수행해보자
9가 1의 부모라면, Explore()의 반환값은 1+1이어야 한다.
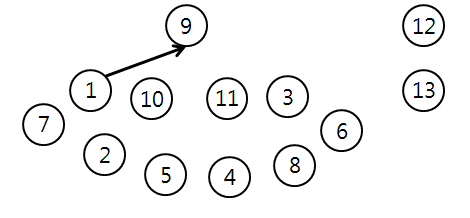
13의 부모를 찾기 위해, TakeKey(13)과 TakeKey(9)를 수행해보자
1이 13의 부모라면 Explore()의 반환값이 2이어야 하지만,
아래 예제에서 반환값은 3이다.
그러므로 13의 부모 후보에서 9는 빠지게 된다.
vec[2]에 들어있는 원소들은 이와같은 방법으로 그래프를 만들 수 있다.
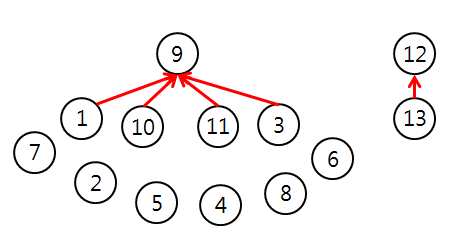
Explore()는 제약이 있기 때문에, 이분 탐색으로 후보를 제거해나가면서 찾으면 된다.
vec[3]도 똑같은 방법으로 부모를 찾을 수 있다.
4의 경우 TakeKey(4)와 TakeKey(1,10,11)을 수행해보자
1,10,11번 방의 부모 9번 방과 4번 방을 포함하여 Explroe()는 5를 반환한다.
그러면 4번 방의 부모는 1,10,11번 중에 있는 것이다.
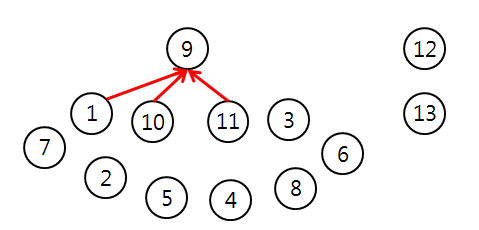
8의 경우 TakeKey(8)과 TakeKey(1,10,11)을 수행했을 때, Explore()는 6을 반환한다.
8번 방 + {1,10,11}번 방 + 부모인 9번 방 = 5와는 예상값이 다르기 때문에, 8의 부모는 1,10,11 중에는 없다.
사이클이 없는 경우는 이분 탐색으로 쉽게 구할 수 있다.
아쉽게도 사이클 제약은 언급되지 않았기 때문에 사이클 예외 처리가 필요하다.
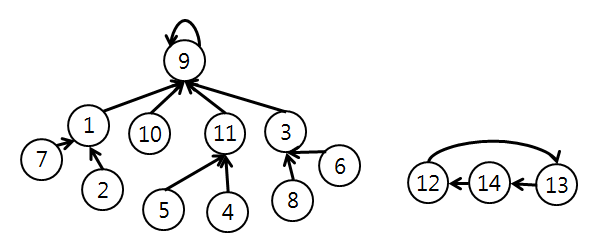
사이클 원소는 사이클의 길이를 c라 할 때, vec[c]에 들어간다.
사이클 원소는 이분 탐색을 사용해도 vec[c-1]에서 부모를 찾을 수 없다.
그래서 부모를 못찾은 경우를 사이클로 간주해도 된다.
사이클 원소의 Explore() 기대값은 c이다.
그래서 사이클 원소 하나를 meta 벡터에 넣고, meta 벡터에서 똑같이 이분탐색으로 사이클 내 부모를 찾을 수 있다.
아래 그림과 같이 meta가 12이고, 14의 부모로 12를 찾을 수 있다.
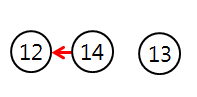
13의 부모를 찾는 과정에서 TakeKey(13)과 TakeKey(meta = 12)를 수행할 수도 있다.
그런데 그래프의 정확한 모양을 찾는 문제가 아니라 13번 방에서 12번 방에 최종적으로 갈 수 있냐 없냐를 찾는 문제이기 때문에 부모로 이어줘도 상관없다.
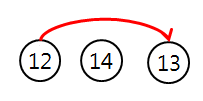
사이클은 여러개가 있을 수 있기 때문에, meta도 벡터로 관리하고 이분 탐색으로 부모 매칭을 해주자
사이클 처리를 한 후, meta의 원소만 vec[c]에 추가해준다.
이는 아래와 같은 경우를 vec[c+1]에서 처리하기 위함이다.
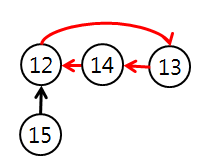
최종적으로 그래프가 완성되면, 모든 i에 대하여 순회 가능한 방을 Report하면 된다.
'Computer Science > PS' 카테고리의 다른 글
| [JOI Spring Camp 2014/2015] 기억 압축 (0) | 2023.04.23 |
|---|---|
| [JOI Spring Camp 2012/2013] 산악 구조대 (0) | 2023.04.23 |
| [IOI17] Cup of Jamshid (0) | 2023.04.23 |
| [JOI Open Contest 2014] Secret (0) | 2023.04.23 |
| [IOI16] Unscrambling a Messy Bug (0) | 2023.04.09 |
- Total
- Today
- Yesterday
- Sqrt Decomposition
- two pointer
- 인터렉션
- DeepLearning
- Joi
- line sweeping
- RMI
- 인터렉티브
- pytorch
- 함수컵
- NERC
- ioi
- Math
- codejam
- boj
- 구간합
- Codeforces
- Book
- greedy
- Decorator
- ICPC
- oj.uz
- LCA
- Divide and conquer
- DataScience
- yaml
- 함수 구현
- TensorFlow
- graph
- Binary Search
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
