티스토리 뷰
문제 : https://codeforces.com/problemset/problem/1666/I
\(n \times m\) 그리드가 있다.
\(nm\)개의 셀 중 두 개의 보물이 파묻혀 있다.
인터렉션을 이용하여 두 개의 보물을 찾는 문제
인터렉션
SCAN \(r\) \(c\)
보물과 \((r,c)\)의 Manhattan distance 합을 입력받을 수 있다.
즉, 두 보물이 파묻힌 좌표가 각각 \((y_1,x_1),(y_2,x_2)\)일 때, \(|x_1-c|+|x_2-c|+|y_1-r|+|y_2-r|\)을 입력받을 수 있다.
두 보물 중 하나 이상을 찾은 경우라도, 두 보물의 원래 좌표와의 거리 합을 입력받는다.
DIG \(r\) \(c\)
\((r,c)\)에서 보물을 찾는다.
\((r,c)\)가 보물이 있는 곳일 경우 1을 입력받을 수 있고, 아니라면 0을 입력받을 수 있다.
제약
- SCAN과 DIG 인터렉션을 합쳐서 최대 7번 호출할 수 있다.
- \(2 \le n,m \le 16 \)
풀이
두 보물이 파묻힌 좌표를 각각 \((y_1,x_1),(y_2,x_2)\)라 하자
SCAN 1 1, SCAN 1 \(m\) 두 인터렉션의 결과 값을 각각 \(i,j\)라 하자
이 때, \(i\)와 \(j\)는 아래와 같이 \(x_1,y_1,x_2,y_2,m\)에 대한 식으로 정의할 수 있다.
$$ i = x_1-1+x_2-1+y_1-1+y_2-1 $$
$$ j = m-x_1+m-x_2+y_1-1+y_2-1 $$
\(i\)에서 \(x\) 관련 항에 대하여는, 아래 그림에서 빨간선과 파란선의 거리 합이 인터렉션의 결과이다.
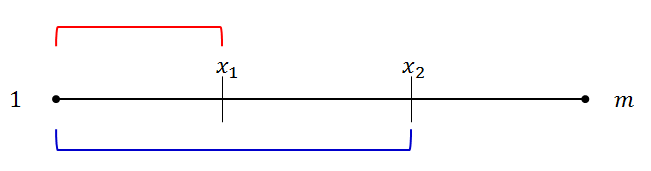
그리고 \(i,j\)두 식을 전개하면 \(x\)와 \(y\)에 대하여 아래와 같이 정리할 수 있다.
$$ x_1+x_2 = { i-j+2+2m \over 2 } $$
$$ y_1+y_2 = { i+j+6-2m \over 2 } $$
그리고 새로운 변수 \(cx=\lfloor{x_1+x_2 \over 2}\rfloor\)를 새로 정의해보자
이 때 \(x_1 \le x_2\)일 경우, \(cx\)는 \(x_1 \le cx \le x_2\)를 만족한다.
그리고 SCAN 1 \(cx\)를 해보자
결과값은 \(cx-x_1+x_2-cx+y_1-1+y_2-1\)이다.
\(x\) 관련 항에 대하여는, 아래 그림에서 빨간선과 파란선의 거리 합이다.
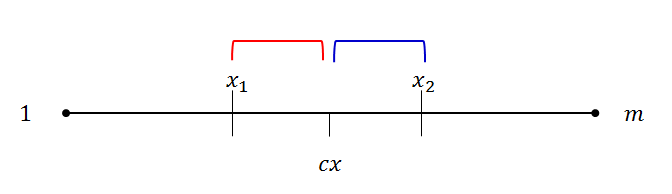
빨간선과 파란선의 거리 합은 \(x_1\)과 \(x_2\)의 거리이기도 하다.
혹은 위 수식을 전개해보아도 SCAN 1 \(cx\)의 결과는 \(x_2-x_1+y_1-1+y_2-1\)가 나오는 것을 어렵지 않게 알 수 있다.
이제 위 수식에서 \(i\)를 빼면 \(x_1\)을 구할 수 있다.
$$ \begin{matrix} x_2-x_1+y_1-1+y_2-1-i \\ =x_2-x_1+y_1-1+y_2-1-x_1-1-x_2-1-y_1-1-y_2-1 \\ = 2x_1-2 \end{matrix} $$
\(cy=\lfloor{y_1+y_2 \over 2}\rfloor\)를 이용하여 , SCAN \(cy\) 1 에서 마찬가지로 \(i\)를 빼면, \(y_1\)도 구할 수 있다.
\(x_1\)과 \(y_1\)을 구하였으니, \(x_2\)과 \(y_2\)를 아래와 같이 정의하자
$$ x_2 = x_1+dx $$
$$ y_2 = y_1+dy $$
그리고, \(i\)와 \(j\)도 다음과 같이 정의할 수 있다.
$$ i = 2(x_1-1)+dx+2(y_1-1)+dy $$
$$ j = 2(m-x_1)-dx+2(y_1-1)+dy $$
\(i\)와 \(j\)를 더하면, \(dy\)를 구할 수 있다.
$$ dy = {i+j-2m-4y_1+6 \over 2}$$
\(dy\)를 구했으면, \(i\) 전개식에서 미지수는 \(dx\)만 남게되어, \(dx\)도 어렵지 않게 구할 수 있다.
4번의 인터렉션으로 \(x_1,y_1,x_2, y_2\)를 구하였다.
보물의 좌표가 \((x_1,y_1),(x_2,y_2)\)라고 가정하여 풀이하였지만,
\((x_1,y_2),(x_2,y_1)\)의 경우에도 위 인터렉션 결과는 똑같이 나온다.
그러므로 DIG \(y1\) \(x1\)의 결과가 1이라면, DIG \(y2\) \(x2\)만 추가적으로 호출하면 되고,
DIG \(y1\) \(x1\)의 결과가 0이라면, DIG \(y2\) \(x1\)과 DIG \(y1\) \(x2\)를 호출하면 된다.
참조
http://nerc.itmo.ru/archive/2021/nerc-2021-tutorial.pdf
'Computer Science > PS' 카테고리의 다른 글
| [Codeforces Global Round 20] notepad.exe (0) | 2022.06.25 |
|---|---|
| [Avito Cool Challenge 2018] Tricky Interactor (0) | 2022.06.22 |
| [Codeforces Round 781] GCD Guess (0) | 2022.06.11 |
| [Codeforces Round 796] Sanae and Giant Robot (0) | 2022.06.08 |
| [JOI Spring Camp 2018/2019] Minerals (0) | 2022.05.25 |
- Total
- Today
- Yesterday
- Sqrt Decomposition
- codejam
- 구간합
- two pointer
- ICPC
- Joi
- pytorch
- oj.uz
- Binary Search
- RMI
- Codeforces
- TensorFlow
- line sweeping
- 인터렉티브
- NERC
- ioi
- greedy
- Divide and conquer
- 함수컵
- Math
- boj
- Book
- LCA
- yaml
- Decorator
- 함수 구현
- DataScience
- DeepLearning
- 인터렉션
- graph
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
