티스토리 뷰
문제 : https://www.acmicpc.net/problem/17679
\(N\)종류의 광석이 있다.
광석 연구를 위해 광석을 2개로 잘랐다.
즉, \(N\)개의 광석들은 \(2N\)개가 되었다.
그런데, \(2N\)개의 광석들을 바닥에 엎어버려서, 그만 섞이고 말았다.
섞여버린 광석들을 같은 종류끼리 짝지어주는 문제
광석이 같은 종류인지 아닌지는 장비를 이용해야 한다.
장비에는 광석을 넣거나 뺄 수가 있다.
장비에 광석을 넣거나 뺄 때마다, 장비에 들어있는 광석 종류의 개수를 알려준다.
\(N=3\)이고, 광석의 인덱스 [ 1 2 3 4 5 6 ]가 있다고 하자
같은 색의 인덱스는 같은 종류의 광석이다.

장비에 1번 광석을 넣으면 장비는 현재 들어 있는 광석 종류의 개수인 1을 반환한다.
이어서 장비에 2번 광석을 넣으면 장비는 현재 들어있는 광석 종류 개수인 2를 반환한다.

이어서 장비에 3번 광석을 넣으면 장비는 현재 들어있는 광석 종류 개수인 2를 반환한다.

이어서 장비에 1번 광석을 뺀다면 장비는 현재 들어있는 광석 종류 개수인 1을 반환한다.

구현해야할 함수
void Solve(int N)같은 광석끼리 짝 지을 수 있도록 구현해야한다.
아래 Answer함수를 이용하여 답을 기록해야 한다.
인터렉션
int Query(int x)x번 광석을 장비에 넣는다. 만약 x번 광석이 장비에 들어있다면, 장비에서 뺀다.
그 후, 장비에 남아 있는 광석 종류의 개수를 반환한다.
\(1\le x \le 2N\)
최대 백만 번 호출할 수 있다.
void Answer(int a, int b)a번 광석과 b번 광석은 같은 종류라고 기록한다.
만점기준 제약사항
- \(N\)은 최대 43000
40점 풀이
Parallel binary search나 분할 정복을 사용하면 된다.
\(2N\)개의 광석을 두 그룹 X와 Y로 나누자.
장비에 광석을 넣었을 때, 반환값이 증가하면 해당 인덱스는 X 그룹으로 넣고,
그렇지 않다면 해당 인덱스는 Y그룹으로 넣는다.
이제 X와 Y그룹에서 각 그룹 내에는 같은 종류의 광석이 존재하지 않는다.
이제 X를 X1과 X2로 이등분하자
장비에 X1만 들어있을 때, Y그룹에 속해있는 광석 y를 넣어보자
이 때 반환값이 증가하지 않는다면, y와 같은 종류의 광석은 X1에 있다.
반환값이 증가했다면, y와 같은 종류의 광석은 X2에 있는 것이다.
모든 y에 대하여, X그룹에서 같은 종류의 광석 범위를 parallel binary search나 분할 정복으로 찾을 수 있다.
100점 풀이
분할 정복을 사용하여 풀어보자.
처음 X와 Y, 두 그룹으로 나누는 것은 똑같다.
그리고 분할 정복을 사용하여, X그룹은 X1,X2로, Y그룹은 Y1,Y2로 나뉠 것이다.
총 4그룹으로 나뉘지만, X1 그룹과 같은 종류의 광석은 Y1 그룹에 있고,
X2 그룹과 같은 종류의 광석은 Y2 그룹에 있다.
이제 여기서 쿼리 사용을 최대한 줄이기 위해 트릭을 좀 사용해보자.
X를 X1와 X2로 나누었지만, 현재 모든 광석들은 여전히 장비안에 들어있다.
장비에서 X를 빼는 것도 비용이 든다.
이 때 다음 연산을 위해 모두 빼는게 아니라, X2만 빼보자
그러면 장비에는 X1과 Y그룹만 들어있다.
모든 y에 대하여 장비에서 광석을 빼보자
쿼리의 반환값이 줄어들지 않는다면, 그 y는 Y1그룹이 된다.
쿼리의 반환값이 줄어들었다면, 그 y는 Y2그룹이 된다.
Y1,Y2도 나누는데 성공했다면, 이제 장비에는 X1만 남는다.
X1도 X11과 X12로 이등분하여 X12만 장비에서 빼고,
이번에는 y를 넣으면서 또 다시 매칭을 해주면 된다.
당연히 y는 장비에 들어있지 않기 때문에 이번에는 쿼리의 반환값의 증가로 매칭해주어야 한다.
X2의 경우 장비에서 빠져있는 상태이므로, X2의 절반만 장비에 넣고, Y2와 매칭해주면 된다.
즉, X의 상태에 따라 절반만 빼거나, 절반만 넣으면 된다.
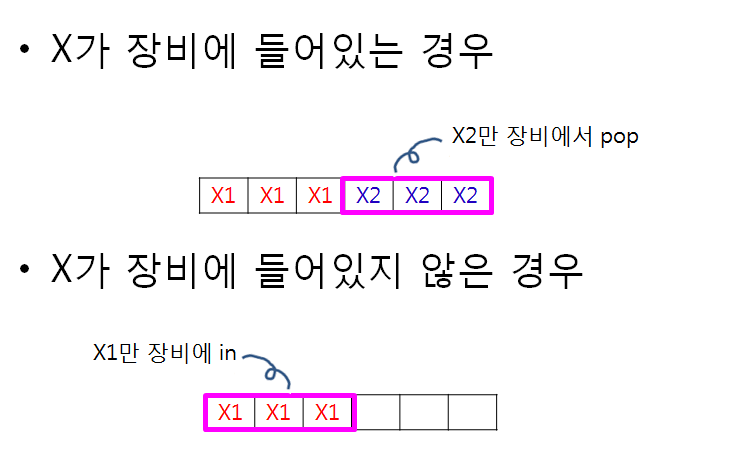
Y 또한 현재 들어있는지 아닌지에 따라, 빼거나 넣으면 된다.
X를 넣거나 빼거나, Y를 넣거나 빼거나 복잡해보이지만, recursive 구조로 구현한다면 어렵지 않다.
하지만 아쉽게도, 이 것만으로는 만점을 받을 수 없다.
만점을 받기 위해 분할 비율 \(p\)를 한 번 생각해보자
기본적인 분할 정복에서 \(p=0.5\)이다.
위에서도 \(p=0.5\)로 예시를 들었다.
하지만 이 문제에서는 \(p=0.5\)가 최적이라고 말할 수가 없다.
광석이 N종류 일 때, Query 호출 수를 \(f(N)\)이라고 하자.
그러면, \(f(N)\)은 다음과 같이 전개할 수 있다.
$$ f(N) = f(pN) + f((1-p)N)+(1+p)N $$
세번 째항 \((1+p)N \)은 X를 넣거나 뺄 때 사용되는 횟수인 \(pN\)과
Y를 Y1과 Y2로 나누기 위해 사용되는, \(N\)을 계산한 항이다.
이제 \(f(N)=tNlogN\)으로 치환해보자
분할 정복이니, \(NlogN\)꼴과 비슷한 횟수가 나올 것이고,
\(t\)는 아직 미지수니 변수로 놓자
그러면 위 수식은 아래와 같이 전개할 수 있다.
$$ \begin{matrix} f(N) = f(pN) + f((1-p)N)+(1+p)N \\ \iff tNlogN = tpNlog(pN) + t(1-p)Nlog((1-p)N) + (1+p)N \end{matrix} $$
위 수식의 왼쪽 항을 오른쪽으로 이동시키면
$$ \begin{matrix} 0 = tpNlogp + t(1-p)Nlog(1-p) + (1+p)N \\ \left(\because tNlogN=tpNlogN+t(1-p)NlogN\right) \end{matrix} $$
위 수식을 \(t\)에 대하여 정리하면 아래와 같이 나온다.
$$ t = { -1-p \over plogp+(1-p)log(1-p) } $$
\(t\)가 \(p\)에 대하여 정리되었다.
이제 \(t\)가 최소가 되는 최적의 \(p\)를 구하자
\(t\)의 도함수 \(t'\)가 0이 되면 된다.
$$ t' = \left ( {-1-p \over plogp+(1-p)log(1-p) } \right)' = 0 $$
이제 위 도함수만 전개하면 된다.
$$ \begin{matrix} \left({-1-p \over plogp+(1-p)log(1-p) } \right)' \\ = plogp + (1-p)log(1-p)-(1+p)(logp-log(1-p)) = 0 \\ \iff 2log(1-p)-logp = 0 \\ \iff {(1-p)^2 \over p} = 1 \\ \iff p^2-3p+1=0\end{matrix} $$
\(p^2-3p+1=0\)에서 근의 방정식을 이용하면 \(p\)를 구할 수 있다.
그런데 \(p\)는 양수이어야 함으로, 최종 \(p\)는 아래와 같다.
$$ p= {3-\sqrt{5} \over 2 } \simeq 0.382 $$
분할 비율 \(p=0.38\)로 두면, \(t=1.44\)가 된다.
즉 X 분할 시, X1과 X2를 0.38:0.62의 비율로 나누면 된다.
그러면 \(O(1.44NlogN)\)번의 연산으로 문제를 풀 수 있다.
\(t\)를 \(p\)에 대하여 정리한 후, 도함수를 이용하여 최적의 \(p\)를 찾았다.
최적의 \(p\)를 찾을 수 있는 다른 방법으로는,
\(p \in (0,1) \)에 대하여, DP를 이용하여 예상 쿼리 호출 수를 구하는 방법이 있다.
참조
https://www.ioi-jp.org/camp/2019/2019-sp-tasks/day4/minerals-review.pdf
'Computer Science > PS' 카테고리의 다른 글
| [NERC 2021] Interactive Treasure Hunt (0) | 2022.06.18 |
|---|---|
| [Codeforces Round 781] GCD Guess (0) | 2022.06.11 |
| [Codeforces Round 796] Sanae and Giant Robot (0) | 2022.06.08 |
| [RMI18] Password (0) | 2022.05.07 |
| [IOI19] Vision Program (0) | 2022.05.02 |
- Total
- Today
- Yesterday
- yaml
- 함수컵
- Divide and conquer
- oj.uz
- codejam
- Math
- TensorFlow
- graph
- ICPC
- two pointer
- LCA
- Binary Search
- DeepLearning
- 구간합
- 인터렉션
- Sqrt Decomposition
- greedy
- RMI
- 인터렉티브
- ioi
- NERC
- Codeforces
- 함수 구현
- pytorch
- Book
- boj
- DataScience
- Decorator
- Joi
- line sweeping
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
