티스토리 뷰
문제 : https://oj.uz/problem/view/JOI17_city
N개의 노드로 이루어진 트리 형태의 나라가 있다.
이 나라의 특징은 0번 도시에서 최대 18개의 도로만을 이용하면 어느 도시로 갈 수 있다.
그래서 많은 사람들이 서로 다른 두 도시 X,Y에 대하여 다음 관계 중 어떤 관계인지 항상 궁금해 한다.
0) 0번 도시에서 X번 도시로 갈 때 Y를 지나치는지
1) 0번 도시에서 Y번 도시로 갈 때 X를 지나치는지
2) 0)과 1) 둘 다 속하지 않는지
모든 서로 다른 두 도시 X,Y는 위 세 조건 중 하나를 만족한다.
X가 0번이라면 Y가 무엇이든 조건 1)이 된다.
나라에서는 복지를 위해 서로 다른 두 도시 X,Y를 쿼리로 주면 위 세 조건 중 하나를 답해주는 기계를 개발하기로 했다.
기계는 다음과 같이 두 종류이다.
Machine 1 : 도로 정보를 참조하여 각 도시마다 한 정수로 인코딩한다.
Machine 2 : 두 도시 X,Y가 Machine 1에서 인코딩된 정수를 입력받아서, 쿼리의 답으로 세 조건 중 하나를 반환한다.
Machine 1과 2 역할을 하는 함수를 구현하는 문제
구현해야할 함수(Encoder.cpp)
void Encode(int N, int A[], int B[])A,B : 길이가 N-1인 엣지 배열
Code() 함수를 이용하여, 각 도시 정보를 정수로 인코딩하는 Machine 1의 역할을 수행하는 함수
한 번만 호출된다.
구현해야할 함수(Device.cpp)
void InitDevice()Machine 2가 작동하기 전 한 번만 호출된다.
필요한 경우 전처리를 수행할 수 있다.
int Answer(long long S, long long T)S,T : Machine 1에서 도시 X,Y가 각각 인코딩된 정수
0에서 X로 가는 경로 중에 Y가 있는 경우 0을 반환한다.
0에서 Y로 가는 경로 중에 X가 있는 경우 1을 반환한다.
X와 Y가 선조-자손 관계가 아닌 경우, 2를 반환한다.
쿼리의 개수 Q개 만큼 호출되며, X와 Y는 서로 다른 도시이다.
인터렉션
void Code(int city, long long code)code : 0이상 \(2^{60}-1\)이하의 정수
city도시를 code로 인코딩한다.
모든 도시마다 한 번씩 호출되어야 한다.
채점
Subtask 1(8점)
- N은 10이하
Subtask 2(92점)
- L을 인코딩된 도시의 code 중 최대값이라고 할 때
- L이 \(2^{38}\)이상인 경우 0점
- \(2^{36} \le L \le 2^{38}-1\)인 경우 10점
- \(2^{35} \le L \le 2^{36}-1\)인 경우 14점
- \(2^{34} \le L \le 2^{35}-1\)인 경우 22점
- \(2^{28} \le L \le 2^{34}-1\)인 경우 \(\lfloor 372-10log_{2}(L+1)\rfloor\)점
- L이 \(2^{28}-1\)이하인 경우 92점
제약
N과 Q는 최대 25만
N=6, Q=5일 때 아래와 같이 호출된다.

풀이
Preliminary
가장 간단한 방법으로 DFS 순회하며 스택에 in, out 시간을 기록하여 간단하게 확인하는 방법이 있다.
\(x\)가 DFS 스택에 들어올 때
in[x]=count++
\(x\)가 DFS 스택에서 나갈 때
out[x]=count
그래서 \(x\)가 \(y\)의 선조라면 아래 조건을 만족하게 된다.
in[x] <= in[y] && out[y] <= out[x]그리고 도시마다 in과 out을 concat하여 인코딩하면 된다.
N은 최대 15만이므로 in과 out은 각각 18개의 비트를 사용한다.
이 때 out대신 out-in 차이값을 인코딩하여 L을 조금이나마 줄일 수 있다.
이럴 경우에 L은 최대 \(2^{36}-1\)이 된다.
만점 풀이
만점을 받기 위해서 L은 \(2^{28}-1\) 이하여야 한다.
그러므로 위 방법에서 인코딩 길이를 더 줄여야 한다.
현재 out-in의 차이값이 최대 25만이기 때문에 18개의 비트를 사용하고 있다.
이를 줄이기 위해 큰 수를 압축하는 방법인 등비수열을 사용해보자
적절한 밑 \(r\)만 정한다면, 지수값으로 치환하여 저장할 수 있다.
등비수열 성질상 지수가 커질수록 값이 기하급수적으로 커지게 된다.
그래서 \(r\)이 1보다 큰 경우에, 실제 값보다 훨신 작은 지수 값을 저장할 수 있게 된다.
하지만 밑 \(r\)이 2인 등비수열을 적용한다해도, out-in의 차이값이 언제나 2의 지수곱 형태이지는 않다.
2가 아니더라도 다른 \(r\)을 정의하더라도 마찬가지 일 것이다.
그래서 더미노드를 추가하여 out-in 차이값을 2의 지수곱 단위로 만든다.
이러면 등비수열을 쉽게 적용할 수 있다.
아래와 같은 트리에서 각 노드의 in/out은 아래와 같이 더미노드를 추가하여, 모든 out-in을 2의 지수곱 단위로 만들 수 있다.
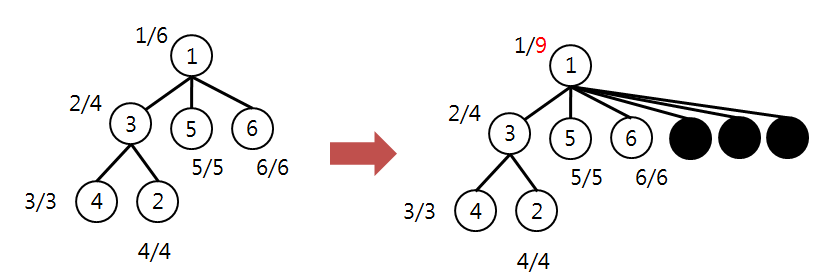
out값은 실제 dfs을 할 필요는 없고, 선형 탐색이나 이진 탐색 등으로 계산할 수 있다.
하지만 \(r=2\)의 경우 문제가 있는데,
out-in의 차이값은 줄었지만, 반대로 in의 인코딩 길이가 증가해버렸다.
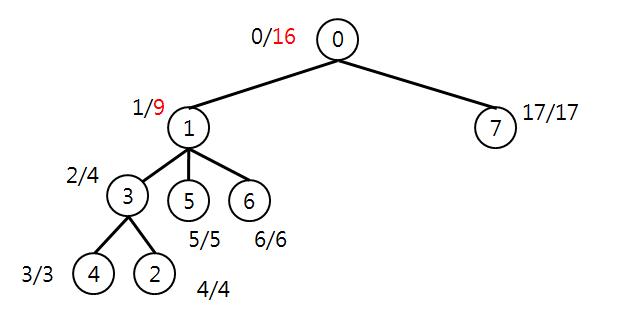
즉, in의 최대값이 기존 N에서 \(Nr^{d}\)가 된 것이다.
(\(d\)는 depth의 최대값)
문제에서 \(d=18\)이고, \(r=2\)로 정했기 때문에, in값만 36개의 비트를 사용하게 되버렸다.
그래서 2가 아닌 다른 \(r\)을 찾아야한다.
그럼 다시 비트단위로 생각해보자
만약 in을 인코딩하는데 K개의 비트를 사용한다면, in의 최대값은 \(2^K\)가 된다.
그리고 \(r\)의 지수의 비트는 만점기준으로 28-K개의 비트를 사용할 수 있다.
그리고 28-K개의 비트를 사용하는 등비수열 \(r\)은 최소 모든 in을 표현할 수 있어야 한다.
그러므로 아래 수식이 세워지게 되고
$$ r^{2^{28-K}} \ge 2^K $$
위 부등호 식에서 좌항에 \(r\)만 남긴다면
$$ r \ge 2^{ ( \frac{K}{2^{28-K}}) } $$
위와 같이 나온다.
이제 \(r=2^{( \frac{K}{2^{28-K}})}\)로 정의하여 가능한 등비수열을 찾아보자.
이 때 K는 최소 18이어야 in을 인코딩할 수 있고, 최대 28까지 가능하다.
가능한 \(r\)에대하여 feasibility를 계산해본다면,
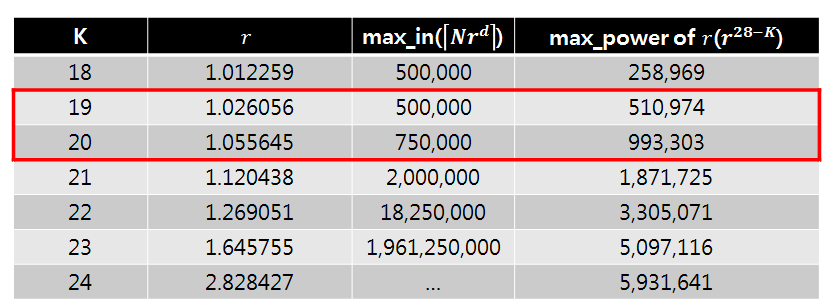
K가 19 혹은 20일 때, \(r\)의 등비수열이 in을 나타내는데 충분함을 알 수 있다.
이제 K=20, \(r=1.055645\)라고 하자.
등비수열 \(a=\{0, r^0, r^1, r^2, ... , r^{254}\}\)이 되는데
\(a\)를 다시 정수로 casting 한다면 \(a\)의 초반 부분은 {0, 1, 1, 1, 1, ...}이 될 것이다.
그래서 중복을 방지하기 위해 \(a_i = max(a_{i-1} +1, a_{i-1} \times r)\)로 계산하자
이제 Encode()에서는 아래와 같이 알고리즘을 수행하면 된다.
- 등비수열 \(a\)계산
- dfs를 수행하여 in과 out을 계산, 이 때 out은 등비수열 \(a\)에 fitting 되도록한다.(lower_bound로 가능)
- 도시마다 K개의 비트는 in을 인코딩, 나머지 28-K개의 비트는 \(a\)의 인덱스가 피팅된다.
Device.cpp에서는
- InitDevice() 함수에서 등비수열 \(a\)를 계산한다.
- Answer() 쿼리마다 S와 T가 주어지면, 비트연산으로 in과 \(a\)의 인덱스를 복원할 수 있다.
- 최종적으로 out을 복원하여, in과 out비교로 선조-자손 관계를 확인할 수 있다.
참조
https://ivaniscoding.wordpress.com/2018/08/28/communication-5-city/
'Computer Science > PS' 카테고리의 다른 글
| [JOI Open Contest 2018] Xylophone (0) | 2023.04.09 |
|---|---|
| [JOI Spring Camp 2017/2018] 항공 노선도 (1) | 2023.04.08 |
| [JOI Open Contest 2017] Amusement Park (0) | 2023.03.26 |
| [IOI17] Coins (0) | 2023.03.01 |
| [JOI Spring Camp 2016/2017] Broken Device (0) | 2023.02.24 |
- Total
- Today
- Yesterday
- 인터렉션
- greedy
- Sqrt Decomposition
- DeepLearning
- Math
- Book
- Decorator
- graph
- LCA
- DataScience
- yaml
- two pointer
- 인터렉티브
- Divide and conquer
- oj.uz
- Joi
- 구간합
- pytorch
- Codeforces
- line sweeping
- 함수컵
- ioi
- Binary Search
- boj
- ICPC
- RMI
- NERC
- 함수 구현
- TensorFlow
- codejam
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
