티스토리 뷰
문제 : https://oj.uz/problem/view/JOI18_airline
N개의 섬과 M개의 항공 노선으로 이루어진 나라가 있다.
그 나라에 사는 Alice는 다른 나라에 사는 Bob을 초대하기 전에 자신의 나라가 어떤 모양인지 알려주기 위해 그래프 정보를 전송하려고 한다.
Alice는 정점의 개수와 엣지 리스트를 전송해주는 telegraph 장치를 이용하여 그래프 G를 전송하려한다.
그런데 이 장치에는 다음과 같은 문제점이 있다.
그래프 G에서 정점의 개수를 V, 엣지의 개수를 U라고 할 때
- 0부터 V-1로 이루어진 임의의 순열 \(p\)가 정해지고, 모든 엣지 \((C,D)\)마다, \((p[C],p[D])\)로 바뀐다.
- 그 후, 0부터 U-1로 이루어진 임의의 순열 \(q\)가 정해지고, 엣지의 순서가 순열 \(q\)에 따라 뒤섞인다.
- \((C_i,D_i)\)는 \((C_{q[i]},D_{q[i]})\)가 된다.
Bob에게는 V와 U, 그리고 두 순열 \(p\)와 \(q\)에 의해 섞여버린 엣지 정보가 전송된다.
Alice는 정점의 개수가 V고, U개의 엣지를 정의한 그래프 G를 전송한다.
이 때, 전송할 그래프 G는 Alice가 사는 나라와 같을 필요는 없다.
Bob이 전송받은 G를 이용하여, Alice의 나라가 어떤 그래프인지 복원하는 문제
구현해야 할 함수(Alice.cpp)
void Alice(int N, int M, int A[], int B[])A,B : 길이가 M인 엣지 정보
인터렉션 InitG 함수와 MakeG 함수를 이용하여 Bob에게 그래프 G 정보를 전송해야한다.
함수가 정료되면 인터렉션으로 생성한 G가 Bob에게 전송된다.
구현해야 할 함수(Bob.cpp)
void Bob(int V, int U, int C[], int D[])C,D : 길이가 U인 그래프 G의 정보, telegraph 장치의 순열 \(p\)와 \(q\)에 의해 셔플되어 있다.
인터렉션 InitMap 함수와 MakeMap 함수를 이용하여 Alice의 나라를 복원해야 한다.
인터렉션
void InitG(int V, int U)그래프 G의 정점의 개수 V와 엣지의 개수 U를 입력한다.
V는 1이상 1500이하이어야 한다.
U는 0이상 \(V(V-1) \over 2\)이하 이어야 한다.
Alice.cpp에서만 호출 가능
void MakeG(int pos, int C, int D)pos번째 엣지 \((C,D)\)를 전송할 그래프 G에 저장한다.
Alice.cpp에서만 호출 가능
void InitMap(int N,int M)Alice의 나라의 N과 M을 기록한다.
Bob.cpp에서만 호출 가능
void MakeMap(int A,int B)Alice의 나라의 엣지 (A,B)를 기록한다.
엣지의 순서는 상관없지만, A와 B는 순열 \(p\)와 \(q\)에 의해 셔플된 번호가 아닌 Alice의 나라의 원래 인덱스와 일치해야 한다.
Bob.cpp에서만 호출 가능
제약
- N은 최대 1000
- M은 최대 \(N(N-1) \over 2\)
- V-N이 12이하이어야 만점을 받을 수 있다.
N=3, M=4일 때 아래와 같은 파이프라인을 가진다.

순열 \(p\)와 \(q\)에 의해 엣지 정보가 셔플된 예시는 아래와 같다.

0번 정점이 2번으로 바뀐 것은 알 수 있지만, 순열 \(q\)에 대해서는 위 예시에서도 알 수 없다.
풀이
MakeMap 함수에서, 섬의 번호는 정확히 입력해야 한다.
그래서 섬의 번호도 정확하게 복원되어야 한다.
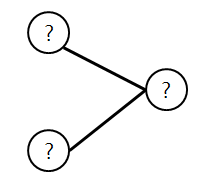
섬 번호를 복원하기 위해 비트 정점을 추가하는 방법이 있다.
Bob은 비트 정점과 열결된 정점의 비트를 on하여 복원할 수 있다.
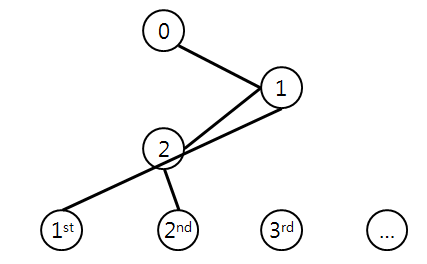
현재까지 V=N+10
하지만 이 비트 정점을 G에 추가해도, 비트 정점도 함께 셔플되기 때문에 비트 정점과 섬을 구분할 수 없게 된다.
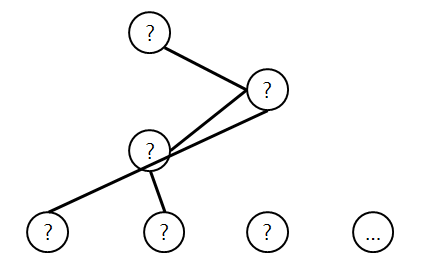
섬을 구분하기 위해 is 정점을 추가하고, 모든 섬은 is 정점과 연결하자
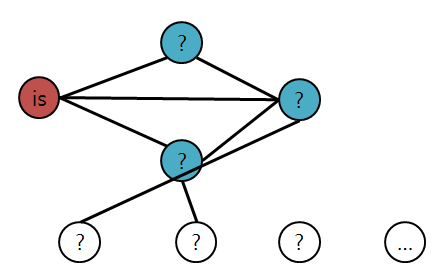
그리고 비트 정점의 순서를 구분하기 위해 1st 정점부터 10th 정점까지 순서대로 엣지를 연결해주자.
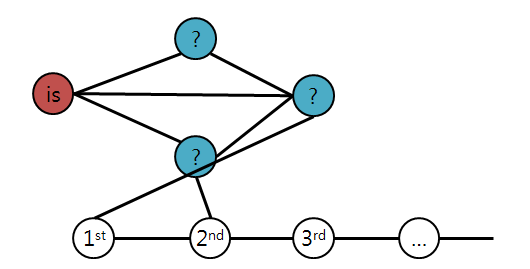
V=N+11이다.
이제 is 정점과 1st 정점만 잘 찾는다면, 섬 번호를 복원할 수 있게되었다.
하지만...
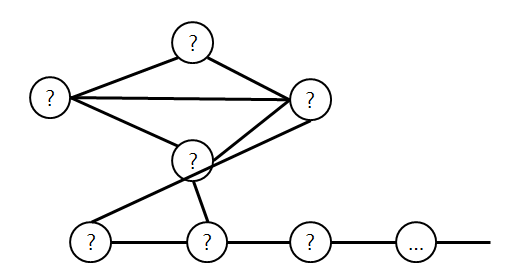
is 정점 역시, 셔플된다.
그래서 is 정점을 구분하기 위해 d1 정점도 G에 추가하자.
d1 정점은 degree가 1인 정점이다.
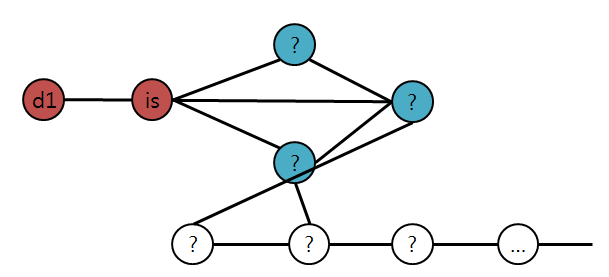
이제 degree가 1인 정점 d1을 찾으면, is도 바로 찾을 수 있다.
하지만 drgree가 1인 정점이 유일하지 않는 경우가 있다.
- 0번 섬의 항공 도로가 없는 경우
- 혹은 N이 1인 경우
이는 모두 0번 섬이 비트 정점에 연결되지 않기 때문에 발생한 문제다.
이를 해결하는 방법은 G 생성시, 0-indexed를 1-indexed로 변경해주면 된다.
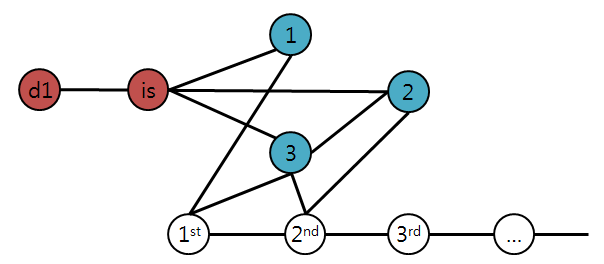
1-indexed가 되었으므로, Bob 함수에서 나중에 0-indexed로 바꾸어주어야 한다.
하지만 아직 degree가 1인 다른 정점이 있다.
N이 512이하 일 때, 10번 비트 정점이다.
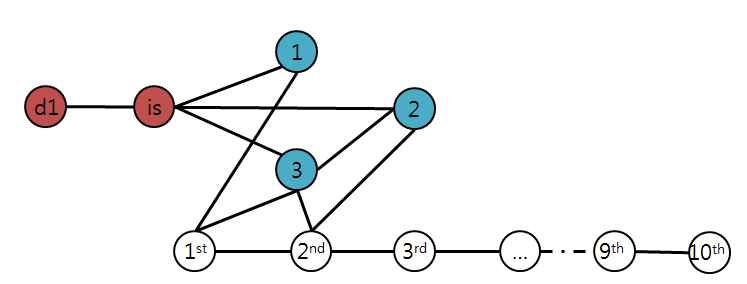
이는 d1 정점의 다음 정점의 엣지가 N+1개인지 체크하여 d1 정점과 is 정점을 찾아낼 수 있다.
is 정점은 모든 섬과 열결되어 있어, N개의 엣지와 d1 정점과의 엣지로 언제나 N+1개의 degree를 가진다.
반면, 10번 비트 정점의 다음 정점인 9번 비트의 경우, degree가 N의 절반 정도이다.
이러한 성질로 엣지의 수를 이용하여 비트 정점도 찾을 수 있다.
[1;N] 까지 비트의 수를 세도 되지만, 1번 비트 정점만 찾고, 비트 정점이 순차적으로 연결된 점을 이용하여, 순회하는 것으로 찾을 수도 있다.
참고로 1번 비트 정점의 엣지 수는 \(\lceil \frac{N}{2} \rceil +1\)개다.
d1 정점, is 정점, 10개 비트 정점을 추가적으로 사용하여 V=N+12로 풀 수 있다.
'Computer Science > PS' 카테고리의 다른 글
| [IOI16] Unscrambling a Messy Bug (0) | 2023.04.09 |
|---|---|
| [JOI Open Contest 2018] Xylophone (0) | 2023.04.09 |
| [JOI Spring Camp 2016/2017] City (0) | 2023.04.01 |
| [JOI Open Contest 2017] Amusement Park (0) | 2023.03.26 |
| [IOI17] Coins (0) | 2023.03.01 |
- Total
- Today
- Yesterday
- two pointer
- Math
- TensorFlow
- 구간합
- pytorch
- RMI
- codejam
- 함수컵
- 인터렉션
- Binary Search
- yaml
- 함수 구현
- DataScience
- LCA
- Book
- oj.uz
- line sweeping
- graph
- 인터렉티브
- Divide and conquer
- ICPC
- Joi
- Sqrt Decomposition
- Decorator
- Codeforces
- NERC
- boj
- DeepLearning
- greedy
- ioi
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
